Hướng dẫn:
 |
- Bài toán 4 được phát triển từ bài toán cơ bản: Yêu cầu tính thời gian gặp nhau khi biết khoảng cách hai chuyển động và vận tốc mỗi chuyển động
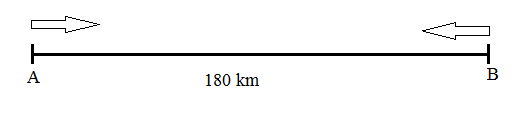
- Bài toán có 2 chuyển động ngược chiều
- 1 mốc thời gian: (cùng một lúc), sau 2 giờ hai xe gặp nhau
- Quãng đường hay khoảng cách của hai chuyển động ngược chiều là: 180 km
- Từ các dữ liệu trên, giáo viên khéo léo hướng dẫn học sinh tính tổng vận tốc của hai xe bằng cách lấy khoảng cách chia cho thời gian gặp nhau (180 : 2 = 90 (km/giờ))
- Sau khi tính được tổng vận tốc hai xe, kết hợp yếu tố bài toán cho biết tỉ lệ vận tốc của hai chuyển động là: 2/3; học sinh vận dụng tiếp bài toán tìm hai số khi biết tổng và tỉ số của hai số đó. Vận tốc của xe đi từ A: 90 : (2 + 3) x 2 = 36 (km/giờ)
Vận tốc của xe đi từ B là: 90 – 36 = 54 (km/giờ)
Bài toán 5: Một xe máy đi từ A lúc 8 giờ 37 phút với vận tốc 36 km/giờ. Đến 11 giờ 7 phút một ô tô cũng đi từ A đuổi theo xe máy với vận tốc 54 km/giờ. Hỏi ô tô đuổi kịp xe máy lúc mấy giờ? (SGK Toán 5, trang 146)
Hướng dẫn:
Đây là bài toán tương đối khó với học sinh, trước khi hướng dẫn chỉ có số ít học sinh làm đúng. Bài toán cho biết rất nhiều dữ liệu: Có hai mốc thời gian, hai vận tốc. Để học sinh hiểu kĩ hơn về bài toán tôi đã dùng phép so sánh toán học. Cụ thể yêu cầu học sinh so sánh với bài toán cơ bản (SGK Toán 5, trang 145).
Sau quá trình Hướng dẫn tìm hiểu học sinh đã rút ra được một số nhận xét sau:
- Hai chuyển động cùng chiều ở trong bài toán cơ bản được xác định trong cùng một thời điểm, còn trong bài toán 4 có hai mốc thời gian.
- Trong bài toán cơ bản đã xác định rõ khoảng cách của hai chuyển động, còn trong bài toán 4 thì không.
=> Như vậy học sinh đã nhìn ra được yếu tố phụ cần phải giải mã đó xác định được mốc thời gian và khoảng cách hai chuyển động.
Giáo viên tiếp tục gợi mở học sinh:
- Ta thử đặt giả thiết xét tại mốc thời gian 8 giờ 37 phút. Tại mốc thời gian này khoảng cách giữa hai chuyển động chưa được xác định.
- Vậy mốc thời gian cần xét là 11 giờ 7 phút.
- Để xác định vị trí của các chuyển động học sinh tiếp tục “giải mã” bằng các phép tính và sự hoạt động của tư duy logíc.
Đến 11 giờ 7 phút xe máy đã đi được thời gian:
11 giờ 7 phút – 8 giờ 37 phút = 2 giờ 30 phút = 2,5 giờ
Sau 2,5 giờ xe máy đi được quãng đường dài:
2,5 x 36 = 90 (km)
Ta có thể minh hoạ bài toán bằng sơ đồ sau:
 |
Đến đây các yếu tố phụ của bài toán đã được giải quyết, học sinh đã đưa được bài toán về dạng cơ bản.
=> Đối với những dạng toán có hai chuyển động như trên, học sinh thường bị rối rắm bởi các dữ liệu bài toán. Cách tốt nhất để hoàn thành bài tập này là hướng dẫn học sinh cách đơn giản bài toán bằng cách đưa bài toán về một mốc thời gian sau đó mới tiếp tục giải
Ngoài ra, sách giáo khoa còn đưa thêm một số bài toán chuyển động xuôi dòng và ngược dòng trong các bài luyện tập, ôn tập cuối năm.
Bài toán 6: Một thuyền máy đi xuôi dòng từ bến A đến bến B. Vận tốc của thuyền máy khi nước lặng là 22,6 km/giờ và vận tốc dòng nước là 2,2 km/giờ. Sau 1 giờ 15 phút thì thuyền máy đến B. Tính độ dài quãng sông AB. (SGK Toán 5, trang 162)
Những kiến thức cần cung cấp cho học sinh:
1) Vận tốc xuôi dòng = vận tốc thực của vật + vận tốc dòng nước.
2) Vận tốc ngược dòng = vận tốc thực của vật - vận tốc dòng nước.
3) Vận tốc thực của vật = (vận tốc xuôi dòng + vận tốc ngược dòng) : 2.
4) Vận tốc dòng nước = (vận tốc xuôi dòng - vận tốc ngược dòng) : 2.
5) Vận tốc xuôi dòng - vận tốc ngược dòng = vận tốc dòng nước x 2.
Hướng dẫn:
- Thực chất đây là bài toán cơ bản dạng tìm độ dài quãng đường khi biết vận tốc và thời gian. Nhưng trong đề bài có thêm một số thuật ngữ mới: “xuôi dòng”, “nước lặng”, “dòng nước”. Để học sinh nắm được kiến thức dạng toán mới mẻ này, giáo viên cần giảng giải kĩ: Vận tốc thực của vật chính là vận tốc của vật khi nước yên lặng.
- Bài toán cho biết chuyển động đang xuôi dòng thì vận tốc của thuyền máy khi xuôi dòng bằng tổng vận tốc thực của thuyền 22,6 km/giờ và vận tốc dòng nước 2,2 km/giờ. (Vận tốc của thuyền máy khi xuôi dòng là: 22,6 + 2,2 = 24,8 (km/giờ))
- Thời gian thuyền máy chạy là:
1 giờ 15 phút = 1,25 giờ
- Sau các bước trên bài toán đã đưa về dạng cơ bản: Tìm quãng đường khi viết vận tốc và thời gian.
- Độ dài quãng sông AB là: 24,8 x 1,25 = 31 (km)
Ngoài việc hình thành bồi dưỡng kĩ năng giải toán, làm tính, quá trình khai thác bài toán còn giúp học sinh tự tin hơn trong cuộc sống. Dạng toán này có sự tích hợp về nội dung kiến thức: Đại lượng thời gian, đại lượng độ dài, các phép toán về số tự nhiên, phân số, số thập phân... Học sinh cũng được củng cố giải các dạng toán khác: Tổng – Hiệu, Tổng – Tỉ, Hiệu – Tỉ, Trung bình cộng, toán trồng cây... Quá trình hoạt động để làm toán học sinh sẽ được hình thành và củng cố khả năng phân tích, tổng hợp, loại bỏ, tư duy lô gíc, tư duy phê phán, đặc biệt là tư duy trừu tượng. Điều quan trọng hàng đầu là hình thành được ở học sinh khả năng tự học, tự tìm tòi, độc lập làm việc, sáng tạo. Đó là những năng lực phẩm chất quan trọng hàng đầu của con người trong thời đại hiện nay – như mục tiêu của Chương trình giáo dục phổ thông 2018.
(Đón đọc phần 2: Các bài toán nâng cao trong sách tham khảo và các kỳ thi)