
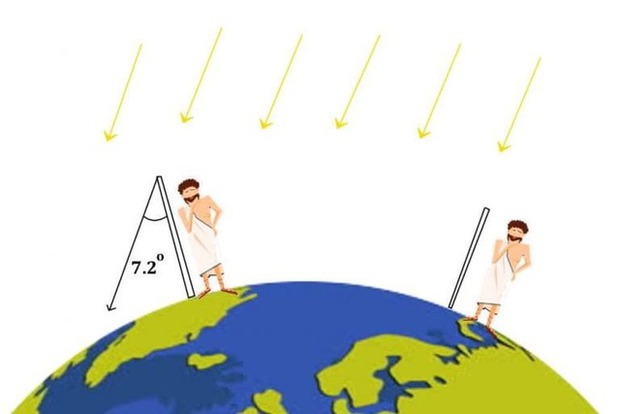
Tiếp theo, ông đo chiều dài của một cây gậy cao gọi là "gnomon" và cắm nó xuống đất ở Alexandria. Khi tia nắng chiếu vào gnomon, nó tạo ra một cái bóng. Bởi vì Mặt Trời chiếu thẳng vào Syrene nên nó phải nghiêng xiên nếu quan sát từ Alexandria. Do đó, người ta có thể quan sát thấy bóng của cây gậy ở Alexandria.
Độ dài của bóng và chiều dài thực tế của cây gậy cho phép Eratosthenes tính được góc nghiêng của Mặt Trời. Điều này có thể được thực hiện bằng cách lấy tang nghịch đảo của tỷ lệ giữa chiều dài của bóng và chiều dài của cây gậy.
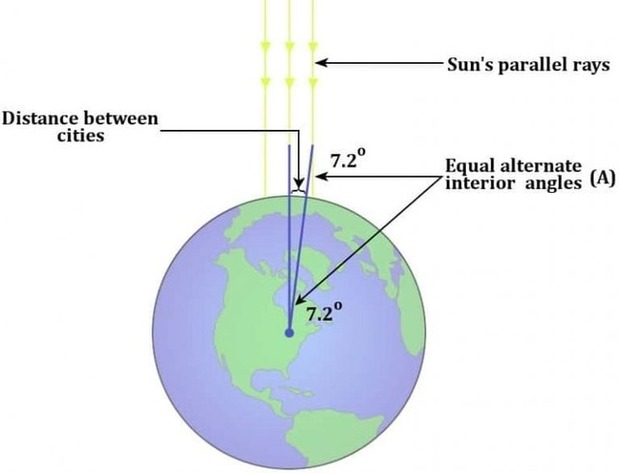
Góc có nhãn "A" được thể hiện trong hình minh họa ở trên. Bằng các quy tắc hình học đơn giản, cũng có thể quan sát thấy A là góc chắn từ tâm Trái Đất với khoảng cách giữa hai thành phố. Góc này được tìm thấy là gần 7,2 độ.
Bây giờ Eratosthenes đã biết góc dự kiến và khoảng cách thực tế giữa Syrene và Alexandria, theo đó ông có thể tính được tổng chu vi của Trái Đất.
Theo các nghiên cứu hiện đại, chu vi theo xích đạo của Trái Đất được tính khoảng 40.075 km, trong khi chu vi theo kinh độ là 40.008 km. Nếu nó là một quả cầu hoàn hảo, chu vi của nó sẽ là 40.030 km.
Khoảng cách giữa Alexandria và Syrene = D km
Góc giữa chúng với tâm Trái Đất = 7,2 độ
Tổng góc của một vòng tròn = 360 độ
Tổng chu vi của Trái Đất= ((360/7,2) x D) km
Đơn vị đo lường phổ biến ở Hy Lạp lúc bấy giờ là stadia (đơn vị được tính theo kích thước của một sân vận động). Các nhà sử học vẫn chưa tìm ra chiều dài thực sự của một sân vận động vào thời điểm đó là bao nhiêu, nhưng các ước tính phổ biến cho rằng nó dài khoảng 160 mét. Eratosthenes ước tính chu vi là 252.000 stadia, xấp xỉ 40.074 km.
Thật đáng kinh ngạc… chu vi theo kinh độ thực sự của Trái Đất chỉ nhỏ hơn ước tính này 66 km! Trái Đất không phải là một hình cầu hoàn hảo và hai thành phố không nằm trên cùng một vĩ độ. Mặc dù phép tính có một chút sai sót, nhưng kỹ thuật nguyên thủy này đã đưa ra câu trả lời chỉ với sai số 0,16%, một con số khá phi thường!
Tham khảo: Scienceabc