 |
| Trò chơi với các que diêm khiến các em hứng thú với phép tính hơn. |
Việc hiểu một con số sẽ trở nên dễ dàng nếu các em biết mỗi con số tự nhiên đều có “câu chuyện” ở ngoài đời, và khi trải nghiệm những thứ đó, lập tức chúng thấy trở nên gần gũi. Chẳng hạn, tôi muốn cho trẻ biết về tính thứ tự, về số liền trước, số liền sau, về so sánh. Tôi không thể áp đặt cho chúng rằng 4 > 3 (vì tụi nó đã bảo tôi 3 cái bánh này lớn hơn 4 cái kẹo đấy!!!). Nhưng khi tôi chơi với chúng trò chơi mua vé tàu hỏa, thì chúng đều biết thứ tự: cậu có vé số 4 à, phải lên sau tớ chứ, vì vé của tớ là số 3. Tụi nó học tự nhiên như thế.
Việc hiểu về các con số giúp tụi nhỏ hiểu ý nghĩa của nó trong phép tính, giúp chúng thực sự học Toán. Khi trẻ học Toán có lời văn, có những tình huống giải quyết vấn đề, chúng chỉ có thể tự tin giải quyết nếu hiểu về các con số đó. Giáo viên dạy Toán tiểu học có kinh nghiệm chia sẻ rằng, học sinh lớp 2, lớp 3, lớp 4 hay mắc sai lầm vì không hiểu cấu trúc số.
Chẳng hạn: “Em có 7 cái kẹo, mẹ cho em thêm 1 chục cái kẹo nữa thì em có bao nhiêu cái kẹo”. Một bạn lớp 2 sẽ có thể trả lời là: 7 + 1 = 8 cái kẹo. Tôi thường khuyến khích các em đặt đề Toán để đố lại giáo viên và các bạn. Việc làm này giúp các em tự tìm thấy Toán học ở xung quanh mình, và bất ngờ hơn, những khái niệm Toán học mà các em thấy khó, thì nhờ việc tự tìm, tự đặt đề bài đã khiến các em chủ động hơn là làm theo các bài toán mẫu mà giáo viên giao cho.
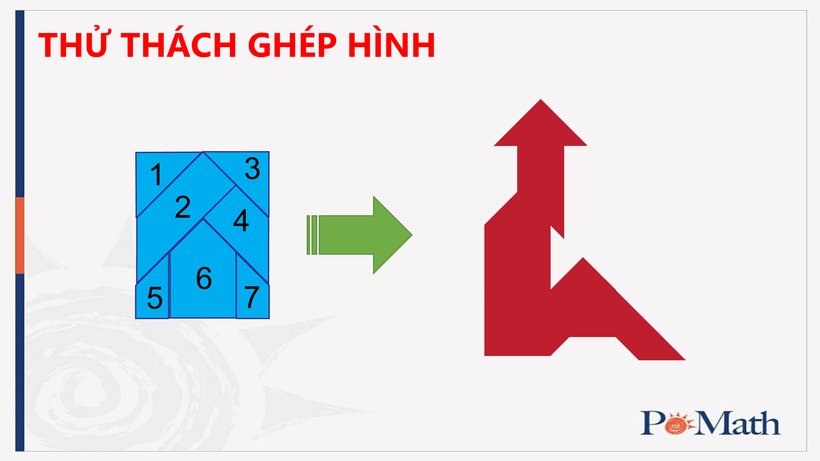 |
| Minh họa: Ghép hình ông già từ 7 mảnh ghép trong bộ Tangram 7 mảnh. |
Nhiều cha mẹ hỏi, tại sao con tôi khi đi học thì chỉ làm những bài cô giáo đã giao, đã chữa. Gặp những bài lạ, câu hỏi lạ, cháu thường lười nghĩ, và chỉ muốn nói cho tôi hiểu: “Con chưa được học bài này”.
Vì sao ư? Có thể bắt nguồn từ chính phụ huynh. Vì chúng ta đã tham vọng kết quả, và cho con bắt đầu học những quy tắc, những bài mẫu mà quên mất, chúng phải mày mò, phải tưởng tượng.
Tượng tượng bắt đầu từ đâu. Đó là cuộc đối thoại của con và cha mẹ, và bạn bè nữa. Kể, mô tả về sự vật, hiện tượng trong mối quan hệ với những thứ khác và với cả những thứ quen thuộc, rồi xa lạ. Chúng tìm thấy những cái mới trong những thứ cũ rích. Chẳng hạn, tưởng tượng ra những thứ xung quanh mình thay đổi thế nào, để diễn đạt, để biện minh, để suy luận. Hình tròn cũng có thể trở thành một hình khác, nếu con kéo chiếc dây chun hình tròn, và nó trở thành hình ovan.
Hình chữ nhật lại biến thành hình vuông, vì con đã bớt di chiều dài của cạnh. Chiếc vỏ lon lăn lông lốc, vì nó tròn. …Con có thể sáng tạo từ 7 mảnh ghép thành hàng nghìn hình khối. Con có thể gấp mảnh giấy thành những ngôi sao, thành những mô hình,…. Sự biến hóa khiến con thấy mình có khả năng vô hạn và thế giới từ vô cùng mà đơn giản như tờ giấy trên tay khi con làm chủ được nó.
Hôm qua, anh bạn học đại học của chồng tôi, một chuyên gia CNTT cố gắng giúp con mình tính diện tích một hình thoi. Cô bé ngại ngần, và sau đó khẳng định rằng con không tính được, vì con chưa được học công thức đó. Anh ấy đã lấy chiếc bút, và nói: Con hãy tưởng tượng, cắt cái hình này ra, ghép thành hình chữ nhật xem sao. Tôi quan sát câu chuyện của bố con anh ấy, và thấy anh ấy đã làm đúng cách. Nhưng vì sao cô bé không thích nghi được, không theo được điều gợi mở của bố. Hóa ra, ở trường, từ rất lâu, con đã không được học như thế. Người ta dạy con luôn công thức, và chỉ thế là hết.
Điều tôi muốn nói ở đây, việc cho trẻ tưởng tượng từ nhỏ quan trọng thế nào. Chúng ta không thể hình thành thói quen tư duy khi chúng lớn được, mà phải là từ rất nhỏ đã được tạo cơ hội để suy ngẫm, mày mò, tự cảm nhận rồi tưởng tượng. Như thế, nếu chúng tìm thấy kiến thức toán học nào, thì kiến thức đó mới bền vững, và chắc chắn, việc làm đó khiến chúng thích thú, say sưa.