Không nên 'đồng phục' việc soạn kế hoạch bài dạy

Sản phẩm:

- Nhận xét cách trình, giải thích tính đúng sai và cho học sinh ghi lời giải vào vở.

- Kết quả: AB ≈ 417m.

Bài 4.Một nhà khảo cổ học tìm được một phần của chiếc trống đồng có bề mặt trống là dạng hình tròn nhưng bị vỡ. Để xác định bán kính của chiếc trống, họ lấy ba điểm A, B, C trên vành trống, tiến hành đo đạc và thu được được số liệu BC = 28cm, góc BAC = 120^o (Hình 2).

Hãy tính bán kính R (lấy một chữ số thập phân) của chiếc trống.

GV: Cho học sinh lên bảng trình bày lời giải.

(gợi ý dùng định lý sin trong tam giác ABC)

HS:

- Thảo luận nhóm để tìm cách tính bán kính R.

- Một học sinh lên bảng trình bày lời giải.

Sản phẩm:

- Nhận xét cách trình, giải thích tính đúng sai và cho học sinh ghi lời giải vào vở.

- Kết quả: R ≈ 16,2cm.

Bài 5. ( Ví dụ SGK trang 76của sách Chân trời sáng tạo)

Hai trạm quan sát ở hai thành phố Đà Nẵng và Nha Trang đồng thời nhìn thấy một vệ tinh với góc nâng lần lượt là 75^o và 60^o (Hình 3). Vệ tinh cách trạm quan sát tại thành phố Đà Nẵng bao nhiêu kilômét? (làm tròn đến hàng đơn vị). Biết rằng khoảng cách giữa hai trạm quan sát là 520km.

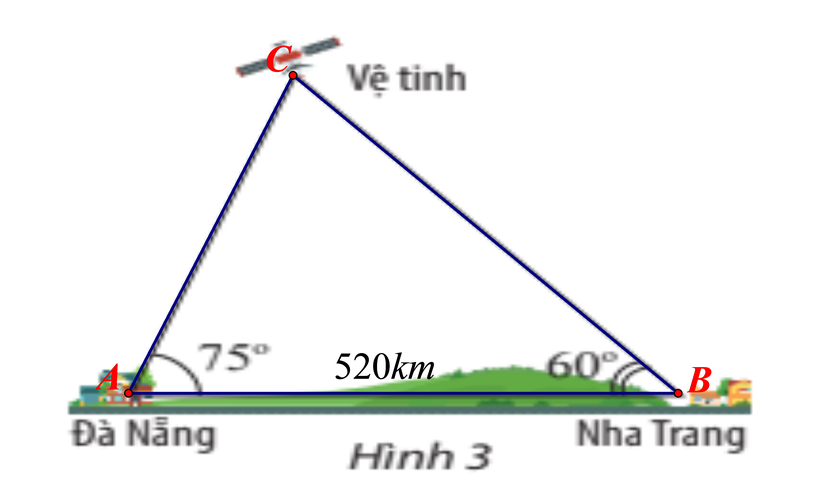GV: Cho học sinh lên bảng trình bày lời giải.

(gợi ý dùng định lý sin trong tam giác ABC)

HS:

- Thảo luận nhóm để tìm cách tính đoạn AC.

- Một học sinh tự nguyện lên bảng trình bày lời giải.

Sản phẩm:

- Nhận xét cách trình, giải thích tính đúng sai và cho học sinh ghi lời giải vào vở.

- Kết quả: góc C = 45^o , AC ≈ 637km.

Bài 6. (Ví dụ 3 SGK trang 75 của sách Chân trời sáng tạo)

Để xác định chiều cao của một toà nhà cao tầng, một người đứng tại điểm M, sử dụng giác kế nhìn thấy đỉnh toà nhà với góc nâng RQA = 84^o, người đó lùi ra xa một khoảng cách LM = 49,4m thì nhìn thấy đỉnh toà nhà với góc nâng RPA = 78^o. Tính chiều cao của toà nhà, biết rằng khoảng cách từ mặt đất đến ống ngắm của giác kế đó là PL. (Hình 2)

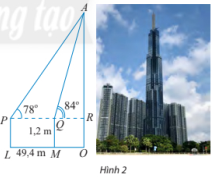GV: Cho học sinh lên bảng trình bày lời giải.

(gợi ý dùng định lý sin trong tam giác ABC)

HS:

- Thảo luận nhóm để tìm cách tính đoạn AO.

- Một học sinh lên bảng trình bày lời giải.

Sản phẩm:

- Nhận xét cách trình, giải thích đúng sai và cho học sinh

ghi lời giải vào vở.

- Kết quả: góc PAQ = C, AR ≈ 460m, AO = 460 + 1,2 = 461,2m.

Bài 7. (Bài 7 SGK trang 77 của sách Cánh diều)

Một người đi dọc bờ biển từ vị trí A đến vị trí B và quan sát một ngọn hải đăng. Phương nghiêng của góc quan sát từ vị trí A, B tới ngọn hải đăng với đường đi của người quan sát là 45^o và 75^o .Biết khoảng cách giữa hai vị trí A và B là 30m (Hình 4). Ngọn hải đăng cách bờ biển bao nhiêu mét (làm tròn đến hàng đơn vị).

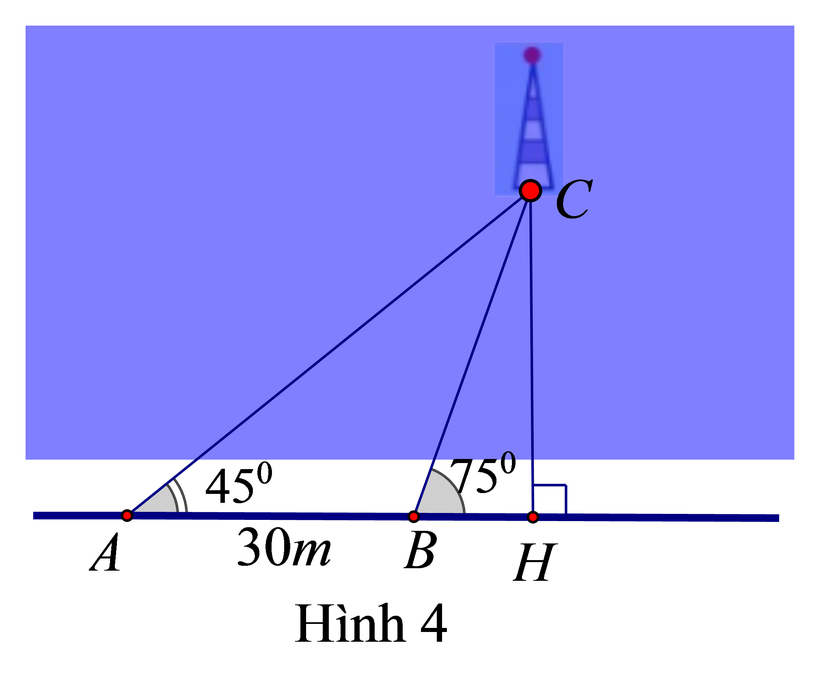GV: Cho học sinh lên bảng trình bày lời giải.

(gợi ý dùng định lý sin trong tam giác ABC)

HS:

- Thảo luận nhóm để tìm cách tính đoạn CH

- Một học sinh tự nguyện lên bảng trình bày lời giải.

Sản phẩm:

- Nhận xét cách trình, giải thích đúng sai và cho học

sinh ghi lời giải vào vở.

- Kết quả: góc ABC = 105^o, góc ACB = 30^o

BD = 30.sin45^o/sin30^o ≈ 42m, CH = BDsin75^o ≈ 41m

4. Củng cố: Giáo viên nhắc lại cho học sinh hiểu giải tam giác và ứng dụng toán học vào thực tế.

5. Hướng dẫn về nhà:

CHUYỂN GIAO NHIỆM VỤ

Phần 1. Trắc nghiệm

Câu 1. Cho tam giác ABC với BC = 5cm, CA = 4cm, AB = 3cm. Khi đó, diện tích tam giác ABC bằng:

A. 12cm²B. 6cm²C. 15cm²D. 10cm²

Câu 2. Cho tam giác có diện tích S = 10cm² và cạnh a = 4cm. Khi đó, đường cao h của tam giác ABC bằng:

A. 20cm B. 4cm C. 5cm D. 10cm

Câu 3. Cho tam giác ABC với BC = a, CA = b, AB = c. Gọi R là bán kính đường tròn ngoại tiếp tam giác ABC. Hãy chọn khẳng định đúng trong các khẳng định sau:

A. a = 3RsinA B. R = a/3sinA C. c = RsinC D. b = 2RsinB

Câu 4. Cho tam giác ABC, với góc A = 30^o, CA = 4cm, AB = 3cm. Khi đó, cạnh BC bằng:

A. 37cm B. √37cm C.13cm D.√13cm

Câu 5. Cho tam giác ABC với góc A = 30^o, BC = 3cm Khi đó, bán kính R của đường tròn ngoại tiếp tam giác ABC bằng:

A. 4cm B. 3cm C. 6cm D. 3/2cm

Câu 6. Hai chiếc tàu cùng xuất phát từ một địa điểm A. Sau 3 giờ, tàu thứ nhất đã đến địa điểm B với quãng đường 130M (130 Hải lý) và tàu thứ hai đã đến địa điểm C với quãng đường 80M (80 Hải lý), biết hướng đi của hai tàu luôn hợp với nhau một góc bằng 120^o (tham khảo hình vẽ dưới).

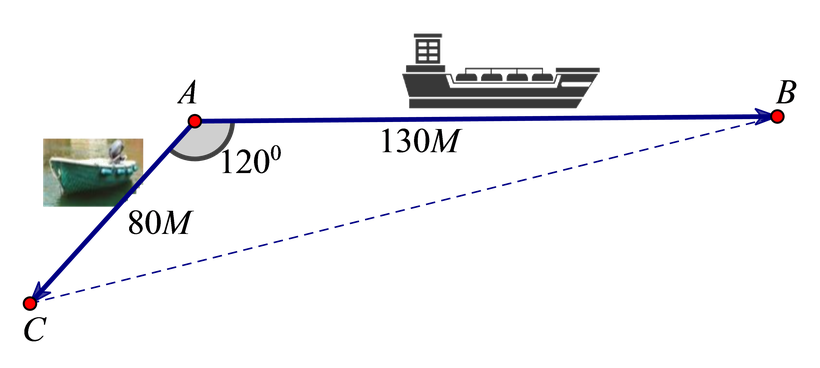Khi đó, hai tàu cách nhau bao nhiêu hải lý ?

A. 10√209M B. 33700M C. 20900M D. 10√337M

Câu 7. Cho tam giác ABC có diện tích S = 8√2 và nửa chu vi P = 4. Khi đó, bán kính R của đường tròn nội tiếp tam giác ABC bằng:

A. √2 B. 4√2 C. 2√2 D. 2

Câu 8. Một nhà khảo cổ học tìm được một chiếc cổ hình tròn nhưng bị vỡ. Để xác định bán kính của chiếc đĩa, họ lấy ba điểm A, B, C trên vành đĩa, tiến hành đo đạc và thu được được số liệu BC = 30cm, góc BAC = 120^o (tham khảo hình vẽ dưới).

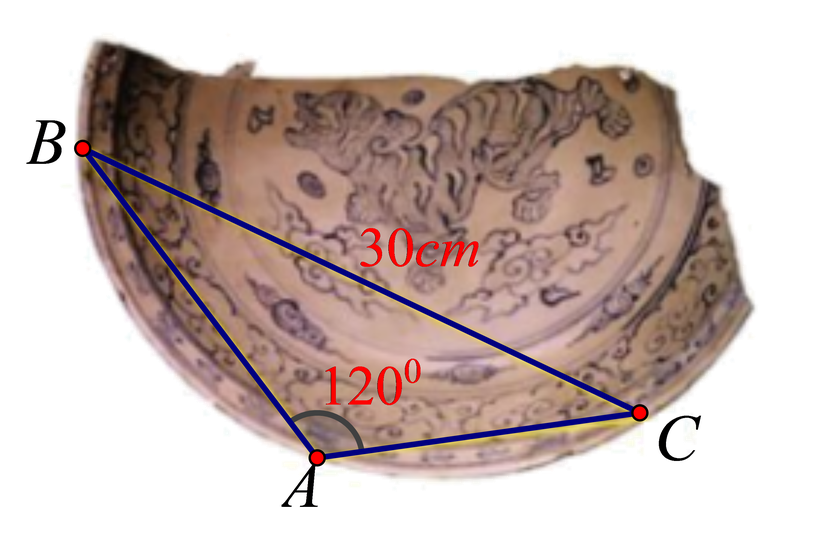Khi đó, bán kính R (lấy một chữ số thập phân) của chiếc đĩa bằng:

A. 16,4cm B. 17,3cm C. 17,8cm D. 18,3cm

Câu 9. Cho tam giác ABC với BC = a, CA =b, AB= c.Hãy chọn khẳng định sai trong các khẳng định sau:

A. cosC = a² + b² - c²/2ab B. cosA = b² + c² - a²/2bc

C. cosB = a² + c² - b²/2ac D. cosB = a² + c² + b²/2ac

Câu 10. Bạn Minh đứng ở vị trí A trên bờ biển để nhìn ra vị trí C của hòn đảo với góc nghiêng là 30^o so với bờ biển. Sau đó di chuyển dọc bờ biển đến vị trí B cách A một khoảng bằng 100m và cũng nhìn về vị trí C với góc nghiêng là 40^o so với bờ biển (tham khảo hình vẽ dưới).

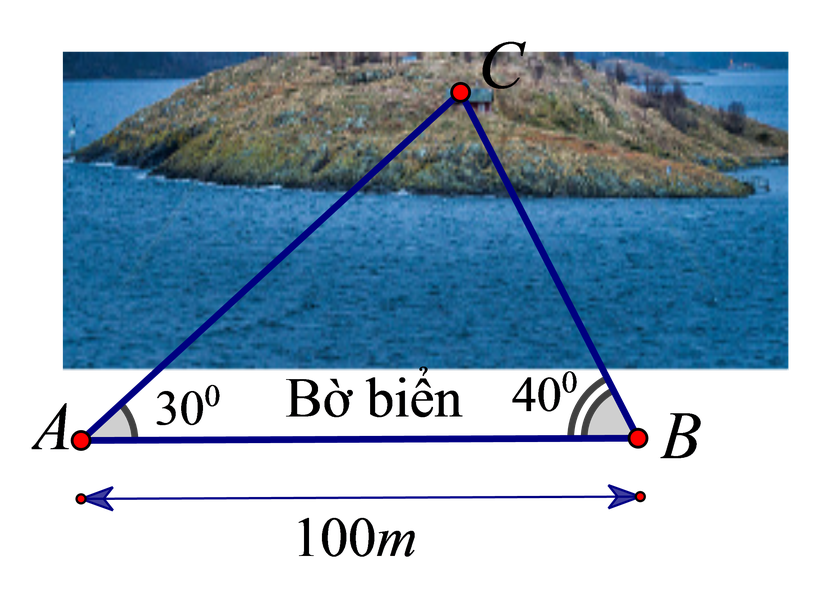Khi đó, độ dài đoạn AC (lấy một chữ số thập phân) bằng:

A. 72,6cm B. 58,6cm C. 78,4cm D. 68,4cm

Đáp án

Phần 2. Tự luận: Giáo viên yêu cầu học sinh làm bài tập trong sách giáo khoa.